1. 가우스 법칙
* 기본 정의
- 어떤 폐곡면을 통과하는 전속은 그 곡면 내에 있는 총 전하량과 같다.
- 전기력선의 밀도를 갖고 전계의 세기를 계산하는 법칙이다.
자!! 지금부터 그림으로 쉽게 알아보겠습니다.
- 어떤 폐곡면을 통과하는 전속은 그 곡면 내에 있는 총 전하량과 같다.
이부분을 그림으로 나타내보겠습니다. 이는 점 P의 전속밀도와 해당면적을 통과하는 총 전속 입니다.

해당 면적 S 부분에서 (단, 폐곡면) 그 부분에서 나가는 전속밀도의 곱은 바로 전속이다! 라고 정의했습니다.
이것이 바로 가우스법칙이며 전속을 구하기 위해 면적과 해당 면적부분에서 발생하는 전속밀도를 알면 전속을 구할 수 있다라는 것을 알 수 있습니다.
자! 그럼 왜 전속을 구하는지 한번 알아보겠습니다.

위의 그림을 보면 전속은 전계속에 양전하와 음전하가 있을때 + -> - 간다는 것을 선으로 표시한 것이 바로 전속입니다.
이러한 전속이 패러데이의 실험에서도 쓰였는데요! <- 이 부분이 key point!!!
패러데이의 실험에 의해 내구에서 더 큰 양전하를 주면 상응하는 외구에 더 큰 음 전하가 유도되며, 전속과 내구의 전하는 정비례한다는 것이 밝혀 졌습니다. 이때 내구로부터 외구로의 일종의 변위가 일어나는데 이때의 속선이 바로 전속입니다. 그러면 여기서 내구 상의 총 전하량을 Q라고 정의한다면 패러데이의 실험 결과 내구의 Q 전하량과 전속은 같다라는 결과가 나왔습니다.

내구의 전하량과 여기서 발생하는 전속이 서로 같다!!! 것을 패러데이 실험에서 밝혀 졌고 이렇기 때문에 전속을 구하면 해당 도체의 전하량 역시 구할 수 있게 되었습니다.

그럼 위의 식은 Q전하량 이다라는 것을 추가할 수 있게 되었습니다.
최종 정리하면 패러데이 실험을 통해 전하량과 전속이 같다 라는 것을 알 수 있었고, 여기에 힘입어 전속을 구하려면 해당 면적과 그 면적에서의 전속밀도를 곱하면 전속을 구할 수있다 라는 가우스법칙이라고 정리할 수 있습니다.
이번에 이 부분을 한번 살펴보겠습니다.
- 전기력선의 밀도를 갖고 전계의 세기를 계산하는 법칙이다.
전기력선의 밀도 : N/S = 전기력선 갯수/면적
전계의 세기 : E
N이 정의되는 과정


이러한 가우스 법칙을 이제 무한 도체 표면, 평면, 평면 사이, 구전하, 동심구, 선전하, 동축 케이블 등에 적용할 것이기 때문에 위의 식을 꼭 기억하고 있어야 됩니다.
우선 이번 포스팅에선 가우스 정리의 적분형과 미분형 포아송의 방정식, 라플라스 방정식에 대해서만 간단히 알아볼 것이며 다음 포스팅에서 가우스 법칙을 활용하여 무한 도체 표면, 평면, 평면 사이, 구전하, 동심구, 선전하, 동축 케이블들의 전계와 전위를 알아볼 것입니다.

**이해를 위한 추가 설명**
막스웰의 제 1 방정식은 가우스 법칙의 미분형 또는 점형식이라고 부를 수 있는데 일반적으로 가우스 법칙은 한 폐곡면을 통해서 밖으로 나가는 전속 수와 폐곡면 내의 전하 사이의 관계를 나타낸 것입니다. 여기서 가우스 법칙의 경우 한 폐곡면이 서로 대칭구조일 경우에만 사용할 수 있는데 이러한 한계점을 극복하기 위해 대칭 구조가 아닐 때 표면(surface)를 점(point)로 극한을 취해 미소체적으로 구하도록 idea를 낸 것입니다.
* 막스웰의 제 1방정식은 가우스 법칙을 미분방정식으로 표시한 것이며, 다른 한편으로 가우스법칙은 막스웰의 제 1 방정식을 적분형으로 표시한 것입니다.
* 여기서 조심해야 될 부분이 가우스 정리의 미분형에서 전하가 있는 곳의 경우 위의 식과 같지만 만일 전하가 없는 곳에선 0이 됩니다.
지금 까진 가우스 정리의 미분, 적분형 이였으며 다음은 포아송과 라플라스 부분입니다.
포아송의 방정식의 경우 "전기력선은 전위가 높은 곳에서 낮은 곳으로 향한다"라는 전기력선의 성질을 이용하는 것입니다.
"전기력선은 전위가 높은 곳에서 낮은 곳으로 향한다" 이 말을 식으로 아래와 같이 표현 할 수 있습니다.
*참고*
전위=전압=전기적인 위치 E에 대한 기본 개념정리
기본정의: 전위를 풀어쓰면 전계의 세기 E인 공간에서 0인 무한 원점에서 점 P까지 전계의 힘을 거슬러서(역방향이라는 의미) 운반하는 일!! 이것이 바로 전위입니다.

이를 위의 그림처럼 기존의 가우스 정리의 미분형에 대입한 식이 바로 포아송의 방정식이며, 만일 전하가 존재하지 않을 때는 이 값이 0이 되는데 이것을 바로 라플라스 방정식이라고 합니다.
지금 부터 가우스법칙 활용을 살펴보겠습니다.
가우스 정리를 활용하여 무한 면, 무한 평면, 무한 평면 사이, 구전하, 동심구, 선전하, 동축 케이블의 전위와 전계를 구해 보도록 하겠습니다.
1. 무한 도체 표면
무한 도체 표면에선 내부에 전하가 존재 할 수 없습니다. 즉, 전계가 없다는 의미입니다.
한쪽 방향으로만 전기력 선이 존재합니다.
2. 무한 평면
도체라는 말이 없습니다.
전기력선이 양쪽 뱡향으로 나갑니다.
3. 무한 평면 사이
평면 사이의 거리 d
전기력선이 한쪽으로만 나갑니다.
위의 내용을 그림으로 나타내면 다음과 같습니다.

위의 경우에서 각각의 전계와 전위가 유도되는 과정은 다음과 같습니다.

4. 구전하
구전하의 경우 점전하를 말하며 구의 넓이 공식 4파이 알제곱을 가우스법칙의 S 부분에 대입하면 쉽게 구할 수 있습니다.
5. 동심구
동심구는 간단히 말해서 구 속에 또다른 구가 있다는 것입니다.
구와 구 사이에는 공기와 같은 절연 물질이 있으며 대전상태가 + -> - -> +로 이루어져 있습니다.
아래의 그림을 보면 이해하기 쉽습니다.

동심구의 내부 전계와 전위 상태를 그래프로 살펴보도록 하겠습니다.
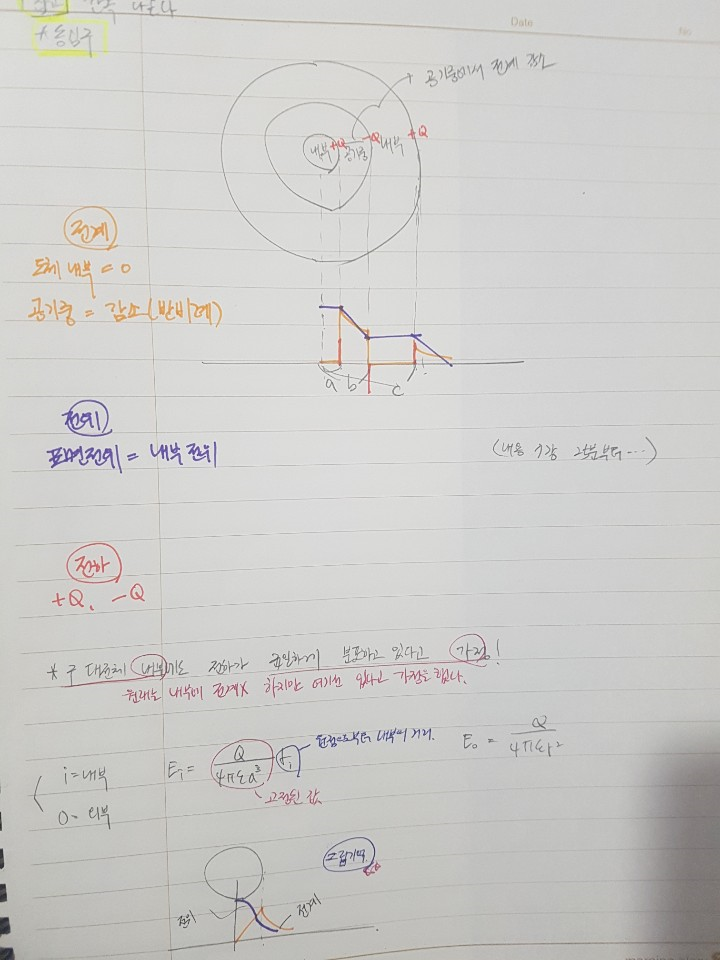
동심구의 전계의 경우 도체 내부는 0이며 공기중은 감소하는 형태를 가지는 반면 전위의 경우 표면전위와 내부 전위가 같은 상태를 가집니다.
주황색 그래프가 전계 그래프 이며 보라색 그래프가 전위 그래프입니다.
6. 선전하
말그대로 선으로 이루어진 전하 입니다.
7. 동축 케이블
동축 케이블은 앞서 설명한 동심구와 같은 형태가 선전하 케이블로 이루어 진것을 말합니다.
그림으로 설명하는 것이 빨라 아래의 필기를 살펴보면서 이해해보도록 하겠습니다.

'전기공학 이야기' 카테고리의 다른 글
| [이론] 단락사고가 발생했을때 단락전류 구하는 법을 알아보자 (0) | 2020.03.16 |
|---|---|
| [이론] 비오 사바르법칙 (Bio Savart Law) 및 1,2,3 차원에 적용 (0) | 2020.01.27 |
| [이론] 암페어의 주회법칙 및 Infinit line과 finit line에서의 자계세기를 구해보자 (0) | 2020.01.25 |
| [이론] 코로나 현상에 대한 설명 (1) | 2020.01.24 |
| [이론] 페란티 현상에 대한 설명 및 방지대책 (0) | 2020.01.23 |


댓글